¿Qué es la materia?
Imagina que sostienes un lápiz, bebes un vaso de agua o incluso respiras aire. ¿Qué tienen en común estas tres acciones? ¡Todas implican materia! La materia es todo aquello que tiene masa y ocupa un lugar en el espacio, y hoy exploraremos las propiedades fascinantes que definen a la materia.
Propiedades Cualitativas: Lo que Percibimos con Nuestros Sentidos
No todas las propiedades de la materia se pueden cuantificar o medir numéricamente, existen características como el color, el sabor, el olor y la textura que dependen de la percepción de nuestros sentidos. Esta forma de describir la materia dificulta el proceso de estandarización de dichas propiedades en un sistema de medición, en consecuencia, que cada ser humano puede tener una percepción diferente de lo que siente, escucha y observa. De las propiedades anteriormente mencionadas tenemos que:
• Color: El color es una propiedad que podemos ver y que nos ayuda a identificar diferentes tipos de materia. Por ejemplo, las fresas son rojas y las hojas de los árboles son verdes. ¿Alguna vez te has detenido a admirar el arcoíris después de una lluvia? Cada color que ves es una propiedad cualitativa de la luz que se refleja en las gotas de agua.
• Textura: La textura describe cómo se siente la superficie de un objeto cuando lo tocamos. Por ejemplo, la suavidad de un cojín de terciopelo o la aspereza de una piedra son ejemplos de texturas que puedes notar con tus manos.
• Olor: El olor es una propiedad que percibimos con nuestro sentido del olfato. Cada tipo de materia puede tener un olor diferente, como el aroma del café recién hecho por la mañana o el olor a hierba recién cortada en el parque.
• Sabor: El sabor es otra propiedad cualitativa que percibimos con nuestra lengua. Piensa en lo diferente que sabe una galleta dulce de una papita salada. Estas diferencias en sabor nos ayudan a disfrutar y distinguir lo que comemos.
Por otro lado, tenemos propiedades de la materia que pueden cuantifiarse como la masa, el volumen, la densidad entre otras. Dichas propiedades física reciben el nombre de magnitudes físicas.
Magnitudes Físicas: Lo que Podemos Medir
Las magnitudes físicas son aquellas que podemos observar y medir sin cambiar su esencia. Estas propiedades nos ayudan a entender mejor el mundo que nos rodea. ¡Aquí te presento algunas de las más importantes!
• Masa: La masa es la cantidad de materia que tiene un objeto. Es una medida de cuánta “sustancia” hay en algo. Por ejemplo, una pelota de fútbol tiene más masa que una hoja de papel porque está hecha de más materia. Piensa en cómo te cuesta más levantar una mochila llena de libros que una vacía; esto se debe a que la mochila llena tiene más masa.
• Volumen: El volumen es la cantidad de espacio que ocupa un objeto. Imagina una botella de agua y un globo inflado. Aunque ambos pueden contener la misma cantidad de aire, el globo tiene más volumen porque ocupa más espacio.
• Densidad: La densidad es una propiedad física de la materia que relaciona la masa con el volumen. Es como preguntar: ¿Qué tan “compacta” está la materia en un objeto? Si comparas un pedazo de metal y uno de madera del mismo tamaño, notarás que el metal es más pesado. Eso se debe a que en el metal hay mayor cantidad de masa por unidad de volumen, es decir, tiene una mayor densidad. Otro ejemplo es un corcho que flota en el agua mientras una piedra se hunde; esto ocurre porque el corcho tiene menor densidad que el agua.
• Temperatura: La temperatura nos dice cuán caliente o fría está la materia, y está relacionada con la energía cinética de las partículas que la componen. Por ejemplo, el agua caliente tiene partículas que se mueven más rápido que las del agua fría, razón por la cual al ingresar un termómetro en una taza de té caliente se observas una mayor temperatura.
• Punto de ebullición y punto de fusión: Estas propiedades hacen referencia a las temperaturas que alcanza la materia para cambiar de estado. Por ejemplo, el agua hierve y se convierte en vapor a 100 °C (punto de ebullición) y se congela en hielo a 0 °C (punto de fusión). Seguro has visto cómo el agua hierve en una olla cuando cocinas pasta o cómo el hielo se derrite en un vaso de limonada en un día caluroso.
En la siguiente actividad aprenderemos que algunas magnitudes físicas tienen intensidad y dirección.
Actividad # 1
Aprendizajes:
• Reconocer que las magnitudes físicas tienen intensidad.
• Reconocer que algunas magnitudes físicas tienen intensidad y dirección.
Ingrese a la siguiente aplicación y reconozca sus funciones
Después de interactuar con la apliación, resuelva los interrogantes de cada fase.
Primera Fase: Sin resistencia del aire y sin agua.
• ¿Qué puede decirse de la velocidad del círculo durante la caída libre?
• ¿Hacia dónde apunta la velocidad del círculo mientras cae?
• ¿Cómo cambia la dirección del movimiento del círculo ?
• ¿Qué se puede decir de la fuerza gravitacional cuando el circulo cae ?
Segunda Fase: Activa la resistencia del aire.
• ¿Qué pasa con la velocidad del círculo cuando aumentan las corrientes de aire? Dibuje un esquema que represente la dirección de las corrientes de aire y la velocidad del circulo.
• ¿Cómo afecta la resistencia del aire a la velocidad del circulo?
• ¿Cómo afecta la resistencia del aire a la intensidad de la velocidad del circulo?
• ¿Cuál es la relación que existe entre la resistencia del aire y la aceleración del círculo? Dibuje un esquema que represente la dirección de la resistencia del aire y la aceleración del circulo.
Tercera Fase: Activa la opción de agua.
• ¿Qué sucede con la velocidad del círculo cuando entra en el agua?
• ¿Hacia dónde se dirige la fuerza de empuje del agua mientras el círculo se mueve hacia abajo? Dibuje un esquema que represente la dirección de la fuerza de empuje del agua sobre el circulo
• ¿Qué se puede decir de la intensidad de la velocidad del círculo mientras este se mueve a través del fluido? Justifica tu respuesta.
• ¿Cuáles son las magnitudes fundamentales y derivadas que intervienen en la experiencia? Explica tu razonamiento.
Antes de continuar, te invito a afinar tus sentidos en la siguiente actividad:
Actividad # 2
Aprendizajes:
• Reconocer que los sentidos pueden engañarnos al caracterizar una propiedad física.
1. Ingresa a la siguiente presentación, resuleve las actividades que allí se encuentran y escribe en el cuadernos una lista de conclusiones sobre aquello que aprendiste.
Pon a prueba tu conocimiento sobre las propiedades de la materia:
Adicionalmente a lo anterior, es de suma importancia mencionar que las magnitudes físicas pueden dividirse en magnitudes escalares y vectoriales.
Magnitudes Escalares y Vectoriales: La Esencia de los Fenómenos Físicos
En nuestro día a día, interactuamos constantemente con fenómenos físicos, ya sea cuando caminamos, conducimos un automóvil o simplemente observamos cómo cae una hoja de un árbol. Detrás de cada uno de estos eventos se encuentran las magnitudes físicas, las cuales nos permiten cuantificar y comprender el mundo que nos rodea. Hoy exploraremos dos tipos fundamentales de magnitudes: las escalaras y las vectoriales.
¿Qué son las Magnitudes Escalares?
Las magnitudes escalares son aquellas que se describen completamente con un solo valor numérico acompañado de una unidad de medida. Este valor nos indica la cantidad de algo, pero no nos dice nada sobre la dirección.
Imaginemos que estás corriendo una maratón. Cuando miras tu reloj, ves que has recorrido 5 kilómetros. Ese número, 5 kilómetros, es una magnitud escalar. No te dice si corriste hacia el norte, hacia el sur o en círculos; solo te dice cuánto has corrido. Otros ejemplos de magnitudes escalares incluyen la temperatura, la masa y el tiempo.
• Temperatura: Si decimos que la temperatura es 25 grados Celsius, no necesitamos saber en qué dirección están esos 25 grados. Simplemente es un número que nos indica cuán caliente o fría está una sustancia.
• Masa: Si un objeto tiene una masa de 10 kilogramos, esta magnitud solo nos dice cuánto material tiene el objeto, sin importar dónde esté o hacia dónde se mueva.
Las magnitudes escalares son fundamentales para entender muchas propiedades de los objetos y sustancias, pero hay situaciones donde también es crucial saber hacia dónde ocurren los fenómenos. Aquí es donde entran las magnitudes vectoriales.
¿Qué son las Magnitudes Vectoriales?
Las magnitudes vectoriales son un poco más complejas. No solo tienen un valor numérico (magnitud), sino que también tienen una dirección. Esto significa que, para describir completamente una magnitud vectorial, necesitamos decir cuán grande es y hacia dónde apunta.
Imaginemos que estás empujando un carrito de supermercado. No solo importa cuánta fuerza aplicas, sino también en qué dirección empujas. Si aplicas 10 newtons de fuerza hacia el norte, el carrito se moverá hacia el norte. Si aplicas la misma fuerza hacia el este, se moverá hacia el este. Esta dirección es una parte integral de lo que significa una magnitud vectorial.
• Velocidad: La velocidad no solo te dice cuán rápido te mueves, sino también hacia dónde te mueves. Por ejemplo, decir que un automóvil se mueve a 60 km/h es solo parte de la historia. Para tener una descripción completa, necesitamos decir si se está moviendo hacia el norte, sur, este o oeste.
• Fuerza: Como en el ejemplo del carrito, la fuerza es otra magnitud vectorial. La cantidad de fuerza y la dirección en la que se aplica determinarán el movimiento del objeto.
¿Por qué Importan las Magnitudes Vectoriales?
Las magnitudes vectoriales son esenciales para entender fenómenos que involucran movimiento y fuerzas. Si alguna vez has volado en avión, el piloto necesita saber no solo la velocidad del avión, sino también la dirección del viento para asegurarse de que el avión llegue a su destino correctamente. Los ingenieros, físicos y otros científicos usan magnitudes vectoriales para diseñar puentes, automóviles, satélites y casi todo lo que implica movimiento o fuerza.
Juego
Aprendizajes:
• Reconocer las magnitudes fundamentales y derivadas.
• Comprender que algunas magnitudes son escalares y otras son vectoriales.
Instrucciones: El juego consiste en localizar las minas que se encuentran ocultas en una cuadrícula de 10x10. Por cada mina descubierta, el equipo obtiene 30 puntos, y en caso contrario, tendrá la oportunidad de ganar 10 puntos si responde correctamente la preguta publicada. Para iniciar, formen dos grupo y elijan al azar quién inicia.
Canción sobre magnitudes escalares y vectoriales
Vectores
¿Qué es un vector?
Un vector se diferencia de una cantidad escalar o numérica por tener asociada una magnitud y una dirección. Los vectores se representan con letras minúsculas y con una flecha en la parte superior como se ilustra a continuación.
Para representar la intensidad de la magnitud física en cuestión, se utiliza el mismo código "fr" y se
elimina la flecha en la parte superior.
Los vectores se representan con una flecha que se compone de longitud, cola y cabeza. La longitud
alude a la intensidad, la cola representa el punto inicial del vector y la cabeza el punto final,
justamente como se aprecia a continuación:
Otro aspecto tan importante como el anterior, es considerar que los vectores pueden moverse a cualquier lugar del plano mediante el uso de rectas paralelas, tal y como se ilustra a continuación:
Las rectas paralelas se usan para garantizar que el vector no modifique su direccción al ser desplazado de un lugar a otro, pues por facilidad en lo que respecta al cálculo de sus componentes rectángulares, se acostubra ubicar la cola del vector en el origen del sistema de referencia. En la siguiente imagen se puede apreciar lo dicho anteriormente:
Las componentes rectángulares de un vector son de gran ayuda para estudiar fenómenos
que se encuentran en dos y tres dimensiones, pues a través de estas,
es posible determinar la distribución de una magnitud vectorial en cada uno de los ejes;
en este caso en partucular, en el eje "x" y en el eje "Y".
Para ejemplificar lo dicho anteriormente, supongamos que el vector "u" descrito en la
gráfica anterior representa la fuerza ejercida por un cuerpo. En este sentido, la longitud o magnitud del vector
hace referencia a la intensidad neta de dicha fuerza, y las componentes rectángulares aluden a la
porción de la intensidad neta que se distribuye en el eje "x" y en el eje "Y". Esto quiere decir, que
la fuerza neta es equivalente a la suma de las fuerzas distribuidas en los respectivos ejes.
Fuerza
¿Qué es la fuerza? Este es un interrogante que cualquier persona puede responder desde su experiencia cotidiana, y si no es así, seguramente sabe como usarla en el diario vivir, puesto que esta magnitud física es necesaria para levantar el maletín del piso, empujar el automióvil cuando falla, al
jugar tira y afloja con la cuerda, al realizar vencidas, entre otras situaciones más.
Las situaciones mencionadas en el párrafo anterior comparten algo en común, y es que
en todos los casos, el maletín, el vaso y el automóvil experimentaron un cambio en el estado de
movimiento como consecuencia de una fuerza aplicada, razón por la cual, definiremos la fuerza como lo hizo Newton en su primera ley: La fuerza es la cuasa de los cambios de movimiento.
Adicionalmente a lo anterior, es importante mencionar que las fuerzas son magnitudes vectoriales, y por esta
razón tienen intensidad y dirección. La intensidad representa la cantidad de fuerza que se imprime sobre un cuerpo,
y la dirección, el ángulo que forman con respecto al eje horizontal.
Un aspecto tan importante como el anterior, es definir los tipos de fuerzas que estudiaremos en este curso:
Fuerzas de contacto
Son las fuerzas que implican un contacto físico entre las partes, como son:
Fuerza normal:Es un fuerza que se caracteriza por ser prependicular a la superificie sobre la
cual se apoya el cuerpo.
Fuerza de fricción: Es una fuerza que va en dirección contraria al movimiento
del móvil y depende del matertial de las superficies en contacto. El nivel de fricción
que puede generar una sperficie puede determinarse a través del coeficiente de rozamiento "μ".
La magnitud o la intensidad de la fuerza de rozamiento puede calcularse como:
fr = μN
Existen otros tipos de fuerzas que no son de contacto, como son :
Tensión: Es la fuerza que experimentan las cuerdas inextensibles y siempre va dirigida hacia el punto de apoyo. Es importante considear que la intensidad de la fuerza se distribuye uniformemente en toda la cuerda, por consiguiente la tensión es igual en todos los puntos.
Fuerza elástica: Es la fuerza que experimentan las cuerdas elásticas, los resortes y cualquier cuerpo que tenga la posibilidad de deformarse y regresar a su estado inicial. La magnitud de esta fuerza puede calcularse con la siguiente expresión:
Fe = -k.x
De la expresión anterior es importante considerar que :
• "-" El signo negativo indica que la fuerza es restitutiva, en otras
palabras, que el resorte tiende a regresar a su posición inicial.
• "k" Representa la constante elástica del resorte.
• "x" Representa la elongación del resorte o su estiramiento.
Peso: Es la fuerza de atracción que ejerce la tierra debido a la acción gravitacional. Esta magnitud física se caracteriza por dirigirse en todos los casos hacia abajo y puede calcularse su intensidad utilizando la siguiente expresión:
W = m.g
Fuerza eléctrica: Es la fuerza que experimentan dos cargas puntuales y depende de la distancia entre ellas y la intensidad de las cargas. Esta fuerza puede ser atractiva cuando las cargas tienen signos diferentes, y repulsiva cuando son del mismo signo. La intensidad de esta fuerza puede calcularse utilzando la siguiente expresión:
Antes de avanzar, es fundamental destacar que tanto la velocidad como la aceleración son magnitudes vectoriales. No obstante, dado que inicialmente nos enfocaremos en las causas del movimiento en lugar del movimiento en sí, centraremos nuestra atención en las fuerzas aplicadas en un sistema. Posteriormente, analizaremos la velocidad y la aceleración como consecuencias directas de las fuerzas aplicadas, tratándolas de la misma manera que cualquier otro vector.
Para analizar las magnitudes vectoriales, es esencial definir un sistema de referencia que permita descomponerlas en sus componentes. Para este propósito, utilizaremos un sistema de coordenadas cartesianas, y llamaremos "diagrama de cuerpo libre" a la representación gráfica de los vectores que actúan sobre un sistema en el plano cartesiano.
Diagramas de cuerpo libre
El diagrama de cuerpo libre es una herramienta importante en la física que se utiliza para representar las fuerzas que actúan sobre un objeto. Este diagrama es esencial para analizar el movimiento de los objetos y comprender cómo las fuerzas influyen en él. En este artículo, explicaremos qué es un diagrama de cuerpo libre y cómo se utiliza en la física.
Un diagrama de cuerpo libre es una representación gráfica de todas las fuerzas que actúan sobre un objeto en un sistema. Se utiliza para aislar el objeto y separarlo del resto del entorno, de manera que solo se consideren las fuerzas que actúan sobre él. En el diagrama, el objeto se representa como un punto y se etiquetan todas las fuerzas que actúan sobre él.
Para crear un diagrama de cuerpo libre, se deben seguir los siguientes pasos:
• Identificar el objeto de interés: el primer paso es seleccionar el objeto
que se va a analizar y aislarlo del resto del sistema.
• Identificar todas las fuerzas que actúan sobre el objeto: después de
identificar el objeto, se deben identificar todas las fuerzas que actúan
sobre él, incluyendo la fuerza de la gravedad, la fuerza normal, la fuerza
de fricción, la fuerza de tensión, etc. Es importante tener en cuenta que
las fuerzas pueden ser tanto internas como externas al sistema.
• Representar las fuerzas en el diagrama: una vez que se han identificado
todas las fuerzas, se deben representar en el diagrama de cuerpo libre.
Cada fuerza se dibuja como una flecha que apunta en la dirección de la fuerza,
con una etiqueta que indica el tipo de fuerza y la magnitud de la fuerza.
• Indicar el sentido positivo: es importante elegir un sentido positivo
para el sistema y etiquetar las fuerzas de acuerdo con este sentido. De
esta manera, se pueden utilizar las ecuaciones para resolver problemas y
encontrar la dirección de la fuerza.
El diagrama de cuerpo libre se utiliza en la física para analizar el movimiento de los objetos. Al aislar el objeto y representar todas las fuerzas que actúan sobre él, es posible determinar la dirección y magnitud de las fuerzas y cómo afectan el movimiento del objeto. Con este diagrama, se pueden aplicar las leyes de la física para encontrar la aceleración y velocidad del objeto.
Para poner en practica lo aprendido hasta este momento, te invito a realizar la siguiente actividad.
Actividad # 3
En cada una de las situaciones planteadas, dibuje un diagrama de cuerpo libre en cada una de las masas y ubique las fuerzas que actúan.
Una vez está claro como se ubican las fuerzas en un sistema y en un diagrama de cuerpo libre, la pregunta obligatoria es: ¿Cómo encuentro la fuerza resultante de un conjunto de fuerzas que actúan en un sistema? La respuesta a dicho interrogante la encontrarán a contiuación:
Calculo de fuerzas y fuerza resultante
La fuerza resultante es la suma vectorial de todas las fuerzas que actúan sobre un objeto en un sistema. En otras palabras, es la fuerza neta que actúa sobre el objeto y lo que determina su aceleración y movimiento en una dirección específica.
Adición entre vectores
El algoritmo de la suma se basa en el principio de traslación y composición de vectores. Este principio establece que para sumar dos o más vectores, se elige uno de ellos como referencia y se trasladan los demás, cuidando que la cabeza de un vector coincida con la cola del siguiente. Esta traslación asegura que los vectores se sumen correctamente, teniendo en cuenta su dirección y magnitud.
Ver el siguiente video para evidenciar lo dicho líneas atrás:
Adición análitica de los vectores
En el siguiente caso deben sumarse los vectortes "u" y "v". El primer paso del algoritmo será seleccionar a "u" como el vector base, luego se traslada "v" mediante rectas paralelas y procurando que la cola de este coincida con la cabeza de "u", tal y como se aprecia en la siguiente imagen:
1
Una vez que se han trasladado todos los vectores, se procede a dibujar el vector resultante. Para ello, se traza una línea recta desde la cola del vector base hasta la cabeza del último vector trasladado. Esta línea representa el vector resultante, el cual tiene una dirección y una magnitud que están determinadas por la suma de los vectores individuales "u" y "v".
2
Es importante destacar que la suma de vectores
es una operación conmutativa, lo que significa
que el orden de los sumandos no
altera el resultado final, por lo tanto, la suma es independiente del orden en que se suman los vectores.
La suma analítica de vectores consiste en
sumar componente a componente las coordenadas cartesianas de los vectores en cuestión, es decir, se suman las componentes "x",
las componentes "y", y en caso de trabajar en tres dimensiones,
las componentes "z". El resultado de esta suma
nos proporciona las componentes del vector
resultante.
Por ejemplo, consideremos los vectores A y B,
con componentes A = (Ax, Ay) y B = (Bx, By). La
suma analítica de estos vectores se obtiene
sumando las componentes correspondientes en
cada eje:
A + B = (Ax + Bx, Ay + By)
En este orden de ideas, para sumar análiticamente los vectores "u" y "v" se realiza la suma componente a compoenente mencionada líneas atrás:
.1
2
Notese que para sumar los vectores "u" y "v" se ubica la cola de "v" sobre la cabeza de "u", de modo que la suma "u+v" está representada con el vector que inicia en la cola de "u" y termina en la cabeza de "v". Por otro lado, puede apreciarse también que la suma análitica entre los vectores "u" y "v" está representada como se indicó líneas atrás, componente a componente. Dicho lo anterior, avancemos en la definición de magnitudes físicas que son vectoriales y veamos como lo aprendidio anteriormente nos ayuda a comprender ciertos fenómenos físicos.
Actividad # 4
Aprendizajes:
• Reconocer que un vector está compuesto por dos componentes rectángulares en el plano cartesiano.
• Aplicar la suma grafica de vectores para determinar la dirección hacia donde apunta la fuerza resultante.
• Calcular la intensidad del vector resultante conociendo las componentes rectángulares.
1. En cada uno de los siguientes graficos:
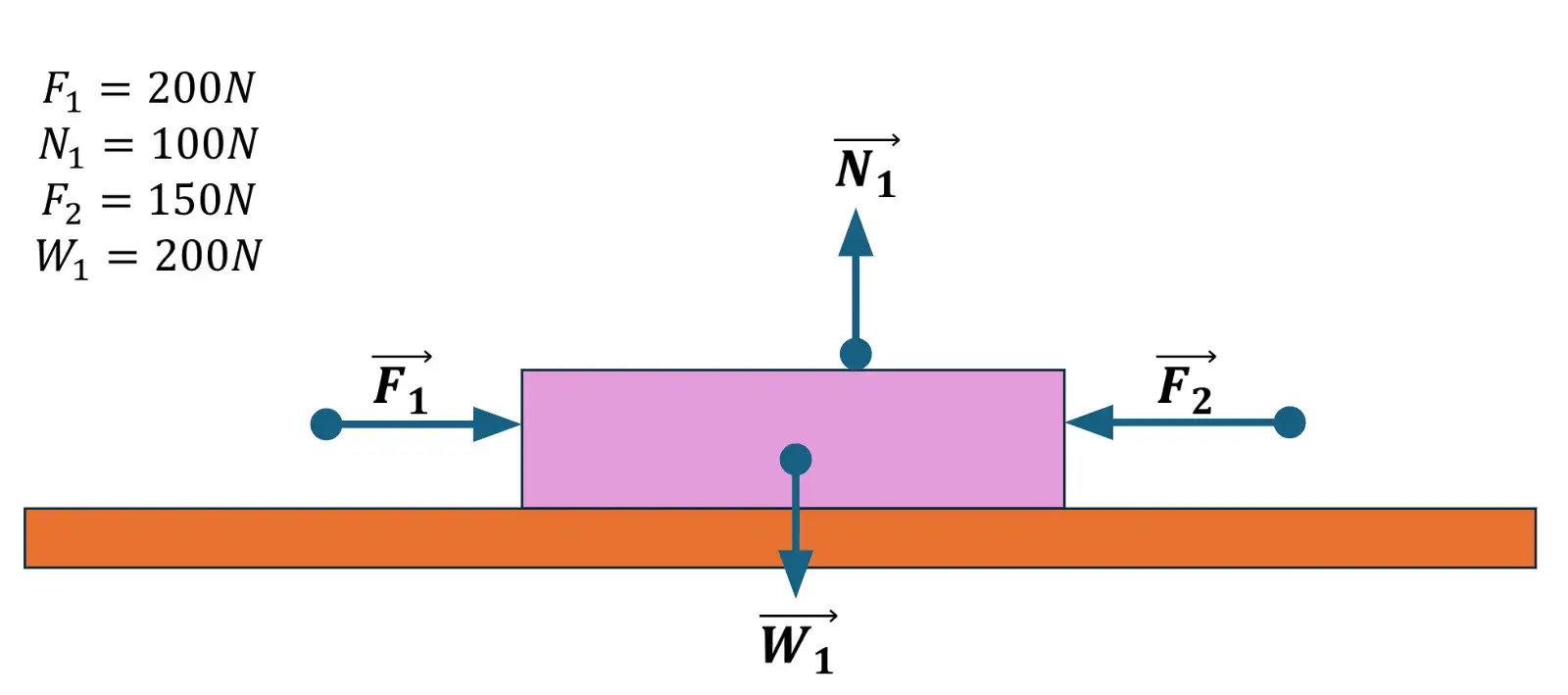Gráfica 4
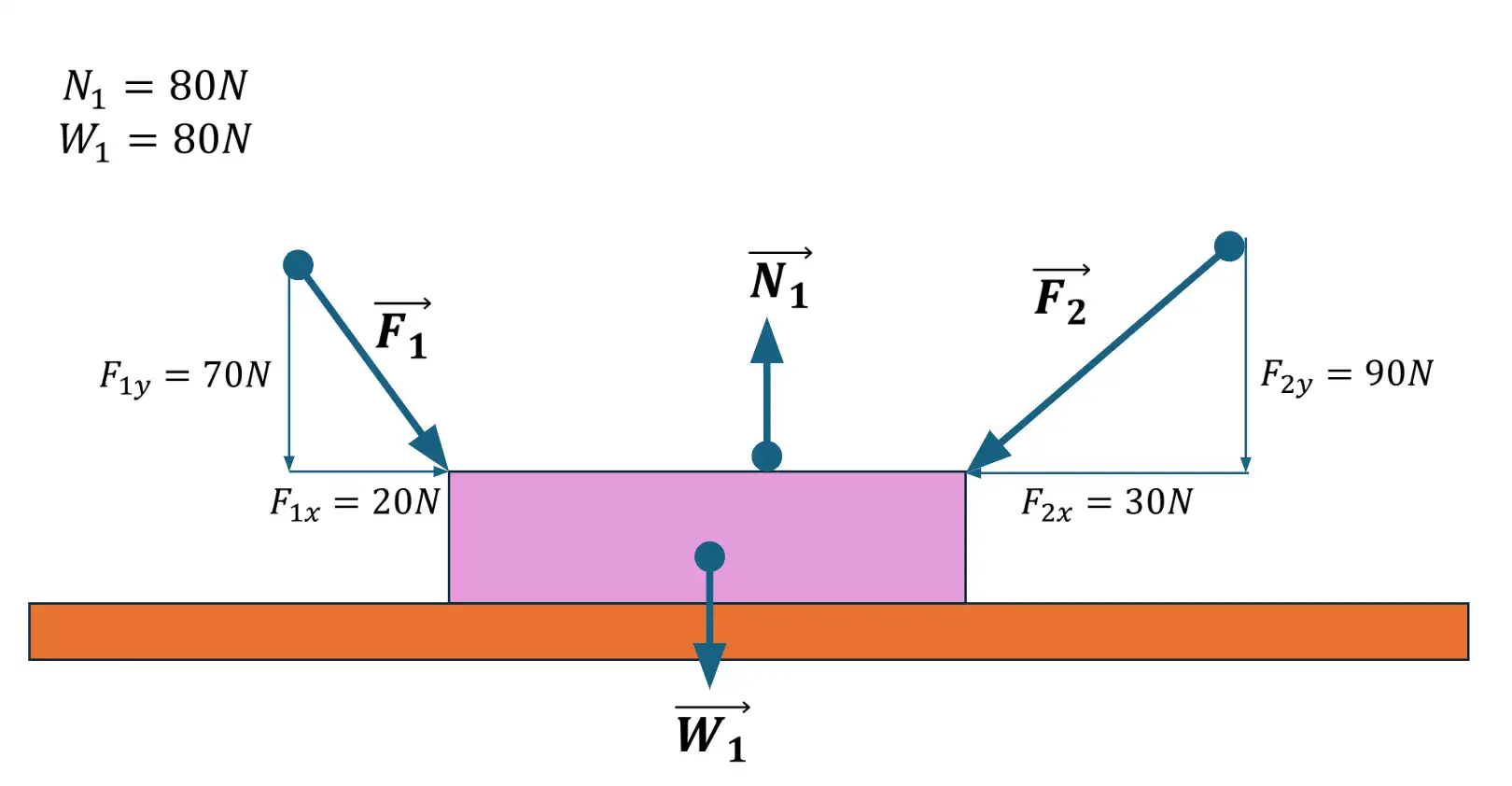Gráfica 3
Gráfica 1
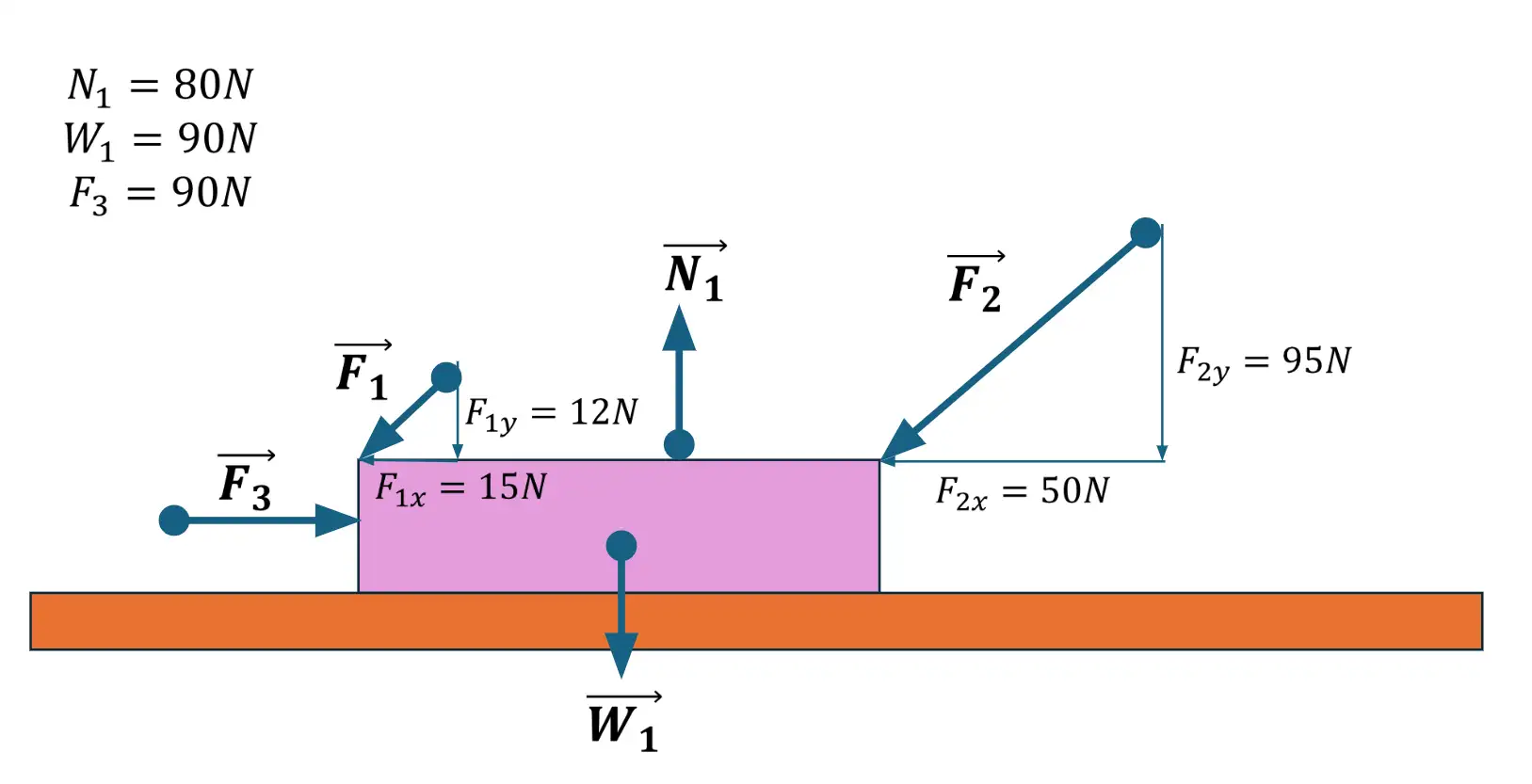Gráfica 2
determine:
• las componentes rectángulares de cada vector.
• la intensidad de los vectores F2 y F1 en las gráficas 1, 2 y 3.
• las componentes rectángulares del vector resultante.
• la intensidad del vector resultante.
• el diagrama de cuerpo libre con todas las fuerzas que actuán en el sistema. Sugerencia: Dibuje el plano cartesiano del tamaño de la hoja, use regla y transportador.
• el diagrama de cuerpo libre, sume los vectores graficamente y encuentre el vector resultante.
Recurso: Observe el siguiente video si tiene dificultades para representar graficamente el vector resultante
2. Ingrese al siguiente recurso y resuelva 10 ejercicios. No olvide registrar en el cuaderno, los ejercicios, los procedimientos y el dibujo del vector resultante.
Actividad # 5
Aprendizajes:
• Identifica y ubica las fuerzas que actuán en una masa.
• Utiliza los diagramas de cuerpo libre para ubicar las fuerzas.
1. Ingrese al siguiente recurso y resuelva las actividades planteadas.
Hasta el momento hemos caracterizado las propiedades de la materia que pueden medirse, aquellas que no y otras que tienen intensidad y direección, sin embargo, está pendiente resolver el siguiente interrogante: ¿En qué y cómo se miden las magnitudes físicas? Para ello, imagina que estás en una misión espacial, desciendes en Marte y te encuentras con un astronauta de otro país. Mientras intentan discutir la distancia a una montaña cercana, ambos se dan cuenta que los datos compartidos difieren en la cantidad y en el patrón de medida utilizado: el astronauta usa millas y tú usas kilómetros, razón por la cual se les dificulta ponerse de acuerdo. Para evitar estos problemas que relacionan ¿En qué se mide?, los científicos crearon el Sistema Internacional de medida (SI), un lenguaje universal que define las magnitudes fundamentales, las magnitudes derivadas y los patrones de medida para facilitar la comunicación entre la comunidad científica.
¿Qué es el Sistema Internacional de Unidades (SI)?
El Sistema Internacional de medida (SI) es un sistema metrológico unificado y estandarizado que permite la coherencia y precisión en la descripción y cuantificación de fenómenos físicos a nivel mundial. Es un conjunto normativo de unidades que posibilita una representación uniforme de magnitudes físicas como la cantidad de materia, la duración de un evento, o la distancia entre dos puntos. De esta forma, se evitan las inconsistencias que puedan surgir debido a la conversión entre sistemas heterogéneos de unidades de medida.
El SI se fundamenta en siete magnitudes fundamentales que actúan como los pilares sobre los cuales se construyen todas las demás unidades derivadas. Estas magnitudes incluyen el tiempo, la masa, la longitud, la intensidad de corriente eléctrica, la temperatura, la cantidad de sustancia y la intensidad luminosa. A partir de estas magnitudes, se pueden derivar unidades que permiten describir prácticamente cualquier fenómeno observado.
Magnitudes Fundamentales: Los Pilares Básicos
Las propiedades fundamentales son aquellas que no dependen de ninguna otra propiedad para ser definidas, en otras palabras, son todas aquellas que pueden medirse directamente. Aquí tienes algunos ejemplos:
• Masa: Se mide en kilogramos (kg) y describe la cantidad de materia en un objeto.
• Longitud: Se mide en metros (m) y representa la distancia entre dos puntos en el espacio.
• Tiempo:Se mide en segundos (s) y cuantifica la duración de un evento o intervalo.
• Intensidad de corriente eléctrica: Se mide en amperios (A) y representa el flujo de carga eléctrica en un circuito.
• Temperatura: Se mide en kelvins (K) y describe la energía cinética de las partículas de un sistema.
• Cantidad de sustancia: Se mide en moles (mol) y cuantifica el número de entidades elementales, como átomos o moléculas, presentes en una sustancia.
• Intensidad luminosa: Se mide en candelas (cd) y expresa la cantidad de luz emitida en una dirección específica por una fuente luminosa.
A partir de estas magnitudes, se pueden derivar unidades que permiten describir prácticamente cualquier fenómeno observado.
Magnitudes Derivadas: Combinando Conceptos
Las magnitudes derivadas, por otro lado, se obtienen combinando dos o más magnitudes fundamentales. Estas propiedades nos dan una visión más completa y detallada de cómo se comporta la materia. Aquí te explico algunas de ellas:
• Densidad: Como vimos antes, la densidad es una propiedad derivada porque se calcula dividiendo la masa de un objeto entre su volumen. Nos dice cuánta materia hay en un espacio determinado. Por ejemplo, si llenas un balón con aire, tendrá una densidad mucho menor que si lo llenas con agua.
• Velocidad: La velocidad es una propiedad derivada que se obtiene dividiendo el desplazamiento de un móvil entre el tiempo transcurrido.
• Aceleración: La aceleración es una propiedad derivada que se obtiene de la razón entre la velocidad y el tiempo.
• Energía: La energía es una propiedad derivada que puede depender de diferentes magnitudes fundamentales según el caso, por ejemplo, La energía potencial gravitacional depende de la altura, mientras que la energía cinética de las velocidad y la energía potencial elástica de la elongación de un resorte.
• Presión: La presión es otra propiedad derivada que se calcula dividiendo la fuerza aplicada entre el área sobre la cual se aplica la fuerza.
El "SI" no solo facilita la comunicación a nivel global, sino que también previene errores significativos en múltiples disciplinas. Un ejemplo ampliamente documentado de cómo la falta de estandarización puede llevar a consecuencias desastrosas es el incidente del Mars Climate Orbiter. Dichos problemas no se limitan únicamente a la exploración espacial, sino que también afectan a industrias como la construcción, la medicina y la ingeniería, donde un error en las unidades de medida puede generar resultados catastróficos. En 1999, el Mars Climate Orbiter se perdió debido a que una parte del equipo empleó unidades del SI, mientras que otra utilizó unidades del sistema imperial (millas y libras). Esta discordancia condujo a la desintegración de la nave al entrar en la atmósfera marciana. Este es solo uno de los muchos ejemplos de los riesgos inherentes a la falta de una convención unificada y estandarizada.
En la siguiente tabla se puden apreciar algunas magnitudes físicas fundamentales, derivadas, el símbolo, el tipo y el instrumento de medida, el cual resuelve la pregunta : ¿Con qué se mide en el sistema internacional de medida?
| Magnitud | Nombre de la Unidad | Símbolo | Tipo | Instrumentos de Medida |
|---|---|---|---|---|
| Longitud | Metro | m | Fundamental | Regla, cinta métrica, calibrador |
| Masa | Kilogramo | kg | Fundamental | Balanza, báscula |
| Tiempo | Segundo | s | Fundamental | Cronómetro, reloj |
| Corriente eléctrica | Amperio | A | Fundamental | Amperímetro, multímetro |
| Temperatura | Kelvin | K | Fundamental | Termómetro, pirómetro |
| Cantidad de sustancia | Mol | mol | Fundamental | Espectrómetro de masas |
| Intensidad luminosa | Candela | cd | Fundamental | Fotómetro, luxómetro |
| Área | Metro cuadrado | m² | Derivada | Planímetro |
| Volumen | Metro cúbico | m³ | Derivada | Probeta, pipeta |
| Velocidad | Metro por segundo | m/s | Derivada | Velocímetro |
| Aceleración | Metro por segundo al cuadrado | m/s² | Derivada | Acelerómetro |
| Fuerza | Newton | N | Derivada | Dinamómetro |
| Energía | Julio | J | Derivada | Calorímetro |
| Presión | Pascal | Pa | Derivada | Manómetro, barómetro |
Para conocer con mayor detalle lo relacionado con el SI haz clic aquí.
Prefijos del Sistema Internacional de Unidades
El Sistema Internacional de Unidades no solo define magnitudes y unidades fundamentales, sino que también utiliza una serie de prefijos para representar múltiplos y submúltiplos de las unidades. Estos prefijos facilitan el manejo de valores extremadamente grandes o pequeños, haciéndolos más fáciles de entender y de utilizar en cálculos científicos y técnicos.
Por ejemplo, en lugar de escribir 1,000 metros, podemos decir 1 kilómetro (km). De manera similar, en lugar de escribir 0.001 gramos, podemos usar 1 miligramo (mg). A continuación, se presenta una tabla con algunos de los prefijos más comunes utilizados en el SI:
| Prefijo | Símbolo | Factor |
|---|---|---|
| Giga | G | 10⁹ |
| Mega | M | 10⁶ |
| Kilo | k | 10³ |
| Hecto | h | 10² |
| Deca | da | 10¹ |
| Deci | d | 10⁻¹ |
| Centi | c | 10⁻² |
| Mili | m | 10⁻³ |
| Micro | μ | 10⁻⁶ |
| Nano | n | 10⁻⁹ |
Actividad # 6
Aprendizajes:
• Realizar conversiones entre unidades de medida.
Ingresa al siguiente recurso, resuelve los ejericicios en el cuaerno y verifica la respuesta ingresando el correspondiente.