Dinámica
Vectores
¿Qué es un vector?
Un vector se diferencia de una cantidad escalar o numérica por tener asociada una magnitud y una dirección. Los vectores se representan con letras minúsculas y con una flecha en la parte superior como se ilustra a continuación.

Para representar la intensidad de la magnitud física en cuestión, se utiliza el mismo código "fr" y se
elimina la flecha en la parte superior.
Los vectores se representan con una flecha que se compone de longitud, cola y cabeza. La longitud
alude a la intensidad, la cola representa el punto inicial del vector y la cabeza el punto final,
justamente como se aprecia a continuación:

Otro aspecto tan importante como el anterior, es considerar que los vectores pueden moverse a cualquier lugar del plano mediante el uso de rectas paralelas, tal y como se ilustra a continuación:

Las rectas paralelas se usan para garantizar que el vector no modifique su direccción al ser desplazado de un lugar a otro, pues por facilidad en lo que respecta al cálculo de sus componentes rectángulares, se acostubra ubicar la cola del vector en el origen del sistema de referencia. En la siguiente imagen se puede apreciar lo dicho anteriormente:

Las componentes rectángulares de un vector son de gran ayuda para estudiar fenómenos
que se encuentran en dos y tres dimensiones, pues a través de estas,
es posible determinar la distribución de una magnitud vectorial en cada uno de los ejes;
en este caso en partucular, en el eje "x" y en el eje "Y".
Para ejemplificar lo dicho anteriormente, supongamos que el vector "u" descrito en la
gráfica anterior representa la fuerza ejercida por un cuerpo. En este sentido, la longitud o magnitud del vector
hace referencia a la intensidad neta de dicha fuerza, y las componentes rectángulares aluden a la
porción de la intensidad neta que se distribuye en el eje "x" y en el eje "Y". Esto quiere decir, que
la fuerza neta es equivalente a la suma de las fuerzas distribuidas en los respectivos ejes.
Considerando que la fuerza neta es equivalente a la suma de las fuerzas distribuidas en
los ejes cartesianos, conviene avanzar hacia las operaciones entre vectores. En este sentido, los vectores
pueden sumarse, multiplicarse con el producto punto y producto cruz. Sin embargo, para efectos de las actividades
que se desarrollarán más adelante, solo es necesario estudiar la suma de vectores.
Fuerza
Es posible que cada persona tenga una noción cotidiana del significado de fuerza, y si no es así,
seguramente tienen claro el uso que le dan en su diario vivir, pues se necesita aplicar fuerza para levantar el maletín del piso, al empujar el automióvil cuando falla, al
jugar tira y afloja con la cuerda, al realizar vencidas, entre otras situaciones más.
Las situaciones mencionadas en el párrafo anterior comparten algo en común, y es que
en todos los casos, el maletín, el vaso y el automóvil experimentaron un cambio en el estado de
movimiento como consecuencia de una fuerza aplicada, razón por la cual, definiremos la fuerza como lo hizo Newton en su primera ley: La fuerza es la cuasa de los cambios de movimiento.
Adicionalmente a lo anterior, es importante mencionar que las fuerzas son magnitudes vectoriales, y por esta
razón tienen intensidad y dirección. La intensidad representa la cantidad de fuerza que se imprime sobre un cuerpo,
y la dirección, el ángulo que forman con respecto al eje horizontal.
Un aspecto tan importante como el anterior, es definir los tipos de fuerzas que estudiaremos en este curso:
Fuerzas de contacto
Son las fuerzas que implican un contacto físico entre las partes, como son:
Fuerza normal:Es un fuerza que se caracteriza por ser prependicular a la superificie sobre la
cual se apoya el cuerpo.

Fuerza de fricción: Es una fuerza que va en dirección contraria al movimiento
del móvil y depende del matertial de las superficies en contacto. El nivel de fricción
que puede generar una sperficie puede determinarse a través del coeficiente de rozamiento "μ".
La magnitud o la intensidad de la fuerza de rozamiento puede calcularse como:
fr = μN

Existen otros tipos de fuerzas que no son de contacto, como son :
Tensión: Es la fuerza que experimentan las cuerdas inextensibles y siempre va dirigida hacia el punto de apoyo. Es importante considear que la intensidad de la fuerza se distribuye uniformemente en toda la cuerda, por consiguiente la tensión es igual en todos los puntos.

Fuerza elástica: Es la fuerza que experimentan las cuerdas elásticas, los resortes y cualquier cuerpo que tenga la posibilidad de deformarse y regresar a su estado inicial. La magnitud de esta fuerza puede calcularse con la siguiente expresión:
Fe = -k.x
De la expresión anterior es importante considerar que :
• "-" El signo negativo indica que la fuerza es restitutiva, en otras
palabras, que el resorte tiende a regresar a su posición inicial.
• "k" Representa la constante elástica del resorte.
• "x" Representa la elongación del resorte o su estiramiento.

Peso: Es la fuerza de atracción que ejerce la tierra debido a la acción gravitacional. Esta magnitud física se caracteriza por dirigirse en todos los casos hacia abajo y puede calcularse su intensidad utilizando la siguiente expresión:
W = m.g

Actividad #1
1. Calcule el peso de la camara, el maletín, la pila de libros y de la manzana en cada caso.
2. Ordene de menor a mayor los resultados obtenidos en el punto anterior.
3. ¿Qué puede concluir del peso?

Fuerza eléctrica: Es la fuerza que experimentan dos cargas puntuales y depende de la distancia entre ellas y la intensidad de las cargas. Esta fuerza puede ser atractiva cuando las cargas tienen signos diferentes, y repulsiva cuando son del mismo signo. La intensidad de esta fuerza puede calcularse utilzando la siguiente expresión:

Antes de avanzar, es fundamental destacar que tanto la velocidad como la aceleración son magnitudes vectoriales. No obstante, dado que inicialmente nos enfocaremos en las causas del movimiento en lugar del movimiento en sí, centraremos nuestra atención en las fuerzas aplicadas en un sistema. Posteriormente, analizaremos la velocidad y la aceleración como consecuencias directas de las fuerzas aplicadas, tratándolas de la misma manera que cualquier otro vector.
Para analizar las magnitudes vectoriales, es esencial definir un sistema de referencia que permita descomponerlas en sus componentes. Para este propósito, utilizaremos un sistema de coordenadas cartesianas, y llamaremos "diagrama de cuerpo libre" a la representación gráfica de los vectores que actúan sobre un sistema en el plano cartesiano.
Diagramas de cuerpo libre
El diagrama de cuerpo libre es una herramienta importante en la física que se utiliza para representar las fuerzas que actúan sobre un objeto. Este diagrama es esencial para analizar el movimiento de los objetos y comprender cómo las fuerzas influyen en él. En este artículo, explicaremos qué es un diagrama de cuerpo libre y cómo se utiliza en la física.
Un diagrama de cuerpo libre es una representación gráfica de todas las fuerzas que actúan sobre un objeto en un sistema. Se utiliza para aislar el objeto y separarlo del resto del entorno, de manera que solo se consideren las fuerzas que actúan sobre él. En el diagrama, el objeto se representa como un punto y se etiquetan todas las fuerzas que actúan sobre él.
Para crear un diagrama de cuerpo libre, se deben seguir los siguientes pasos:
• Identificar el objeto de interés: el primer paso es seleccionar el objeto
que se va a analizar y aislarlo del resto del sistema.
• Identificar todas las fuerzas que actúan sobre el objeto: después de
identificar el objeto, se deben identificar todas las fuerzas que actúan
sobre él, incluyendo la fuerza de la gravedad, la fuerza normal, la fuerza
de fricción, la fuerza de tensión, etc. Es importante tener en cuenta que
las fuerzas pueden ser tanto internas como externas al sistema.
• Representar las fuerzas en el diagrama: una vez que se han identificado
todas las fuerzas, se deben representar en el diagrama de cuerpo libre.
Cada fuerza se dibuja como una flecha que apunta en la dirección de la fuerza,
con una etiqueta que indica el tipo de fuerza y la magnitud de la fuerza.
• Indicar el sentido positivo: es importante elegir un sentido positivo
para el sistema y etiquetar las fuerzas de acuerdo con este sentido. De
esta manera, se pueden utilizar las ecuaciones para resolver problemas y
encontrar la dirección de la fuerza.
El diagrama de cuerpo libre se utiliza en la física para analizar el movimiento de los objetos. Al aislar el objeto y representar todas las fuerzas que actúan sobre él, es posible determinar la dirección y magnitud de las fuerzas y cómo afectan el movimiento del objeto. Con este diagrama, se pueden aplicar las leyes de la física para encontrar la aceleración y velocidad del objeto.
Para poner en practica lo aprendido hasta este momento, te invito a realizar la siguiente actividad.
Actividad # 2
En cada una de las situaciones planteadas, dibuje un diagrama de cuerpo libre en cada una de las masas y ubique las fuerzas que actúan.






Una vez está claro como se ubican las fuerzas en un sistema y en un diagrama de cuerpo libre, la pregunta obligatoria es: ¿Cómo encuentro la fuerza resultante de un conjunto de fuerzas que actúan en un sistema? La respuesta a dicho interrogante la encontrarán a contiuación:
Calculo de fuerzas y fuerza resultante
La fuerza resultante es la suma vectorial de todas las fuerzas que actúan sobre un objeto en un sistema. En otras palabras, es la fuerza neta que actúa sobre el objeto y lo que determina su aceleración y movimiento en una dirección específica.
Adición entre vectores
El algoritmo de la suma se basa en el principio de traslación y composición de vectores. Este principio establece que para sumar dos o más vectores, se elige uno de ellos como referencia y se trasladan los demás, cuidando que la cabeza de un vector coincida con la cola del siguiente. Esta traslación asegura que los vectores se sumen correctamente, teniendo en cuenta su dirección y magnitud.
Ver el siguiente video para evidenciar lo dicho líneas atrás:
Adición análitica de los vectores
En el siguiente caso deben sumarse los vectortes "u" y "v". El primer paso del algoritmo será seleccionar a "u" como el vector base, luego se traslada "v" mediante rectas paralelas y procurando que la cola de este coincida con la cabeza de "u", tal y como se aprecia en la siguiente imagen:
1

Una vez que se han trasladado todos los vectores, se procede a dibujar el vector resultante. Para ello, se traza una línea recta desde la cola del vector base hasta la cabeza del último vector trasladado. Esta línea representa el vector resultante, el cual tiene una dirección y una magnitud que están determinadas por la suma de los vectores individuales "u" y "v".
2

Es importante destacar que la suma de vectores
es una operación conmutativa, lo que significa
que el orden de los sumandos no
altera el resultado final, por lo tanto, la suma es independiente del orden en que se suman los vectores.
La suma analítica de vectores consiste en
sumar componente a componente las coordenadas cartesianas de los vectores en cuestión, es decir, se suman las componentes "x",
las componentes "y", y en caso de trabajar en tres dimensiones,
las componentes "z". El resultado de esta suma
nos proporciona las componentes del vector
resultante.
Por ejemplo, consideremos los vectores A y B,
con componentes A = (Ax, Ay) y B = (Bx, By). La
suma analítica de estos vectores se obtiene
sumando las componentes correspondientes en
cada eje:
A + B = (Ax + Bx, Ay + By)
De manera similar, para sumar más de dos
vectores, se suman las componentes
correspondientes de cada vector en cada eje.
En el siguiente gráfico se puede apreciar un ejemplo de lo mencionado anteriormente:
1

2

Notese que para sumar los vectores "u" y "v" se ubica la cola de "v" sobre la cabeza de "u", de modo que la suma "u+v" está representada con el vector que inicia en la cola de "u" y termina en la cabeza de "v". Por otro lado, puede apreciarse también que la suma análitica entre los vectores "u" y "v" está representada como se indicó líneas atrás, componente a componente. Dicho lo anterior, avancemos en la definición de magnitudes físicas que son vectoriales y veamos como lo aprendidio anteriormente nos ayuda a comprender ciertos fenómenos físicos.
Para continuar profundizando en las causas del movimiento, es necesario abordar las tres leyes de Newton. Isaac Newton (1642-1727) fue un físico, matemático y astrónomo inglés que es considerado uno de los científicos más influyentes de la historia. Su trabajo en mecánica clásica sentó las bases para gran parte de la física moderna. Newton formuló las tres leyes fundamentales del movimiento, que describen cómo los cuerpos responden a las fuerzas aplicadas. Estas leyes, conocidas como las tres leyes de Newton, son fundamentales para entender y analizar el comportamiento de los objetos en movimiento y han tenido un impacto significativo en el desarrollo de la ciencia y la ingeniería.
Actividad # 3
Aprendizajes:
• Identifica y ubica las fuerzas que actuán en una masa.
• Utiliza los diagramas de cuerpo libre para ubicar las fuerzas.
1. Ingrese al siguiente recurso y resuelva 10 ejercicios. No olvide registrar en el cuaderno los ejercicios, los procedimientos y el dibujo del vector resultante.
2. Ingrese al siguiente recurso y afiance lo aprendido sobre la ubicación de fuerzas en el diagrama de cuerpo libre.
Leyes de Newton
Primera ley de Newton - Inercia
La primera ley de Newton enuncia que todo cuerpo mantiene su estado de movimiento inicial hasta que una fuerza externa actúa sobre él y cambie su estado de movimiento, tal y como sucede con el carrito de color rojo al colisionar con el obstáculo de plástico, o con Mangüirry al colisionar contra el piso después de ser lanzado por inercia. Te invitamos a ver el desenlace de esta situación haciendo play en el siguiente video.
Dos jugadoras de Rugby que continuan moviéndose por inercia después de colisionar una contra la otra, representa otro ejemplo de la primera ley de Neton. La pregunta siguiente podría ser ¿Cuándo pierden su inercia y se detienen? Cuando lleguen al suelo y una fuerza externa (la fricción) actúe sobre ellas.
A continuación encontrarán un enlace que les permitirá descargar un archivo en pdf con actividades útiles para practicar lo aprendido. Haz clic aquí para descargar la guía de actividades.
Segunda ley de Newton - Ley de proporcionalidad.
La segunda ley de Newton, también denominada ley de proporcionalidad, relaciona dos aspectos naturalmente diferentes: por un lado, las interacciones o causas del movimiento, y por otro, los efectos de dichas interacciones. Esta ley establece que la aceleración de un objeto es directamente proporcional a la fuerza neta que se aplica sobre él e inversamente proporcional a su masa, describiendo así cómo la fuerza aplicada afecta al cambio en el movimiento del objeto.
En consecuencia a lo anterior, si tenemos una fuerza resultante de 10N que genera una aceleración constante de 10m/s² y duplicamos la fuerza aplicada, tendremos que la aceleración producida también será el doble e igual a (20m/s²), y en el caso contrario que dupliquemos la aceleración, tendremos que la fuerza aplicada también se duplicará y su valor será de 20N.
Con el propósito de involucrar la primera ley de Newton en el desarrollo conceptual de la segunda ley, formulemos la siguiente pregunta: ¿Cuál es la causa que produce cambios en el movimiento de un cuerpo? Para responder esta pregunta es muy útil acudir a nuestra cotidianidad, pues todos hemos sido testigos alguna vez del efecto de las fuerzas sobre el estado de movimiento de los cuerpos. En este sentido, cada vez que deseamos levantar un objeto, moverlo, detenerlo o arrastrarlo, acudimos a la fuerza para cambiar el estado de movimiento de los cuerpos, en otras palabras, cambiamos su estado de inercia.
El estado de movimiento de un cuerpo cambia cuando se le aplica una fuerza externa que desestabiliza el sistema y genera un incremento en la aceleración. Esto quiere decir que la magnitud de la fuerza resultante deja de ser cero y por ende rompe el estado de inercia del cuerpo. Analíticamente es posible representar el equilibrio o el estado de inercia de un cuerpo si igualamos a cero el producto de la masa por la aceleración “ m . a = 0 Newtons” o igualamos la fuerza resultante a cero “ ΣF = 0 Newtons.
Desde una perspectiva más coloquial, podríamos decir que un cuerpo cambia su estado de inercia, si y solo sí experimenta un empujón (Cualquier fuerza externa) que desequilibre el sistema y por ende cambie su movimiento, de lo contrario podemos afirmar que el cuerpo mantiene su inercia o conserva su estado de movimiento inicial.
Observemos el siguiente video y veamos qué sucede cuando duplicamos la fuerza aplicada y la masa del objeto.
Tercera ley de Newton - Acción y reacción.
En esta ley es importante considerar que la acción y la reacción son dos fuerzas que tienen la misma línea de acción, actúan en direcciones puestas y sobre cuerpos diferentes. Esta ley permite comprender situaciones cotidianas como el dolor que experimentamos al golpear la pared con las manos desnudas o al patear un balón de fútbol con los pies descalzos. Cuando golpeamos la pared con las manos desnudas o aplicamos una acción sentiremos dolor instantáneamente como consecuencia de la reacción que efectuó la pared sobre nosotros.
En el siguiente video se presenta un sistema en equilibrio, en el cual se calcula la intensidad de las fuerzas que actuán sobre las cuerdas que sostienen una caja que pende de ellas. Para ello, se aplcian las tres leyes de Newton y el diagrama de cuerpo libre. Los invito a verlo para conocer en detalle la solución del respectivo problema.
Es hora de poner en practica lo aprendido hasta este momento, por esta razón, te invito a resolver la siguiente actividad:
Actividad # 4
1. Resuelva los siguientes recursos en orden ascendente.
2. Considerando que se desprecia la fricción y que el sistema está en equilibrio, calcule el valor de la tensión en "A", "B" y "C" cuando m1= 80Kg

Si deseas practicar más ejercicios como este, ingresa al siguiente test
3. Considerando que el sistema está en equilibrio, calcule el valor de la tensión en "A", "B" y la fricción cuando m1= 60Kg y m2= 60Kg

Si deseas practicar más ejercicios como este, ingresa al siguiente test
4. Considerando que se desprecia la fricción y que el sistema está en equilibrio, calcule el valor de la tensión en "A", "B" y "C" cuando m1= 70Kg, α = 50° y β = 40°.

Si deseas practicar más ejercicios como este, ingresa al siguiente test
5. Considerando que el sistema está en equilibrio, calcule el valor de la tensión en "A", "B", "C", la fricción y el valor de la masa m2 cuando m1= 700kg y β = 50°.

6. Considerando que se desprecia la fricción y que el sistema está en equilibrio,
calcule el valor de la tensión en "A", "B", "C", "D", "E" y el valor de la masa
m2, cuando m1= 50kg,
β = 50° y α = 48°.

Si deseas practicar más ejercicios como este, ingresa al siguiente test
7. Considerando que se desprecia la fricción y que el sistema está en equilibrio, calcule el valor de la tensión en "A", "B", "C" y "F" cuando m1= 50kg, β = 38° y α = 42°.

Actividad # 5
1. Mangüirry estudia el movimiento de un bloque sobre un plano incliando como el que se muestra en la siguiente imagen:

y para ello formula las condiciones de la experiencia, un interrogante de investigación y sus respectivos objetivos:
Condiciones de la experiencia:
• Despreciar la fricción.
Interrogante de investigación: ¿Cómo modelar
matemáticamente la velocidad que experimenta el cuerpo de masa "m"
que desliza sobre un plano cuya inclinación es 30°?
Objetivos general: Modelar matemáticamente
la velocidad que experimenta el cuerpo de masa "m" que desliza
sobre un plano cuya inclinación es 30°.
Objetivos específicos:
• Dibujar un diagrama de cuerpo libre y ubicar las fuerzas que actuán sobre la masa "m".
• Calcular la fuerza resultante.
• Aplicar la segunda ley y calcular la aceleración de la masa "m".
• Diligenciar la tabla N°1.

• Representar los datos de velocidad y tiempo en un diagrama (V vs t).
• Construir una ecuación que represente el comportamiento de los datos del gráfico (V vs t).
a. Lea cuidadosamente cada uno de los objetivos que plantea Mangüirry y desarrollelos
ordenadamente en el cuaderno.
b. Utilice la ecuación construida y calcule la velocidad del bloque al cabo de 2s, 3.5s y 4.2s.
c. Construya una lista de conclusiones.
Actividad # 6
1. Mangüirry estudia el movimiento de dos bloques que deslizan sobre dos rampas que tienen la misma altura pero difieren en el ángulo de inclinación con la horizontal, tal y como se muestra en la siguiente imagen:

Para iniciar su investigación formula las condiciones de la experiencia, un interrogante de investigación y sus respectivos objetivos:
Condiciones de la experiencia:
• Despreciar la fricción.
• La rampa que tiene una base de 40m forma un ángulo de 14° con la horizontal.
• La rampa que tiene una base de 7m forma un ángulo de 55° con la horizontal.
Interrogante de investigación: ¿Cuál es el bloque que llega primero a la parte inferior de la rampa y cuál experimenta la mayor velocidad en dicho punto?
Objetivos general: Identificar el bloque que llega primero a la parte inferior de la rampa y calcular las velocidades de cada uno.
Objetivos específicos:
• Dibujar un diagrama de cuerpo libre en cada una de las masas y ubicar las fuerzas que actuán.
• Calcular la fuerza resultante en cada una de las masas.
• Aplicar la segunda ley y calcular la aceleración de la masa que experimenta en cada una de las masas.
• Diligenciar la tabla N°1 y N°2.

• Representar los datos de velocidad y tiempo de cada masa en un diagrama (V vs t).
• Construir una ecuación que represente el comportamiento de los datos de cada gráfico (V vs t).
a. Lea cuidadosamente cada uno de los objetivos que plantea Mangüirry y desarrollelos
ordenadamente en el cuaderno.
b. Utilice la ecuación construida y calcule la velocidad del bloque al cabo de 2s, 3.5s y 4.2s
c. Construya una lista de conclusiones.
Actividad # 7
Mangüirry recibe un informe de laboratorio en el cual se encuentra el siguiente gráfico cartesiano:

Considerando que las condiciones de estudio descartan la fricción.
a. Utilice la información suministrada para completar la tabla N°1 y luego realice una lista de conclusiones que describan el movimiento del objeto de estudio.

b. Calcule la fuerza resultante si el cuerpo en cuestión tiene una masa de 2kg.
Actividad # 8
Mangüirry recibe un informe de laboratorio en el cual se encuentra el siguiente gráfico cartesiano:

Considerando que las condiciones de estudio descartan la fricción.
a. Utilice la información suministrada para completar la tabla N°1.

b. Suponiendo que el informe de laboratorio refiere al movimiento vertical de un cuerpo ¿Cuál es la dirección del movimiento del cuerpo? c. ¿Cuál es el peso del cuerpo? d. ¿Cuál es la masa del cuerpo? e. ¿Cuál es el valor de la gravedad? f. Redacte una lista de conclusiones que describan el movimiento del objeto de estudio.
Actividad # 9
Resuelva el siguientes test y practique lo aprendido
Actividad # 10
1. Mangüirry estudia el movimiento de una esfera que desliza sobre un plano inclinado como se mueestra en la siguiente gráfica:

Para iniciar su investigación formula las condiciones de la experiencia, un interrogante de investigación y sus respectivos objetivos:
Condiciones de la experiencia:
• Despreciar la fricción entre las superficies.
• No hay aire.
Interrogante de investigación: ¿Como predecir y caracterizar matemáticamente la posición de la esfera en "X" e "Y" respecto al tiempo?
Objetivos general: Predecir y caracterizar matemáticamente la posición de la esfera en "X" e "Y" respecto al tiempo.
Objetivos específicos:
• Identificar las magnitudes físicas fundamentales que intervienen en la experiencia.
• Medir las magnitudes fundamentales y registrar los datos en una tabla.

• Elegir la operación matemática pertinente para correlacionar los datos registrados.
• Identificar el tipo de correlación que existe entre los datos.
• identificar el comportamiento de los datos y construir un modelo matemático que los represente.
Utiliza la información suministrada y resuelve los siguientes puntos:
a. Describa el comportamiento de los datos en ambos ejes y diga si son directos, inversos o proporcionales.
b. ¿Cuál es la gráfica que describe el comportamiento de los datos en ambos ejes? Diga si es líneal o cuadrática.
c. Escriba el modelo matemático que describe la correlación entre la posición y el tiempo en ambos ejes.
d. Sí la pelota recorre toda la rampa en 4.22s ¿Cuánta distancia recorrió la esfera?
e. Calcule la posición de la pelota en el eje "X" cuando han transcurrido 2.5s.
f. Calcule la posición de la pelota en el eje "Y" cuando han transcurrido 2.5s.
g. ¿Cuál es la aceleración que experimenta la esfera?
Actividad # 11
Ingrese al siguiente recurso y encuentre el valor de la gravedad de cada uno de los planetas propuestos.
Actividad # 12
Ingrese al siguiente recurso y aplique lo aprendido sobre el movimiento, las causas del movimiento y el teorema de la conservación de la energía.
Teorema de la conservación de la energía mecánica
Sistemas conservativos
Un sistema conservativo es aquel en el que, en ausencia de fuerzas disipativas como la fricción o la resistencia del aire, la energía mecánica total (la suma de la energía cinética y potencial) se mantiene constante. Esto ocurre porque las fuerzas que actúan en el sistema son conservativas, lo que significa que el trabajo que realizan depende únicamente de los puntos inicial y final del movimiento, permitiendo definir una energía potencial. Ejemplos típicos de fuerzas conservativas son la gravedad y la fuerza elástica. En contraste, cuando intervienen fuerzas no conservativas, parte de la energía mecánica se transforma en otras formas, como calor, haciendo que la suma de la energía cinética y potencial ya no se conserve.
Fuerzas conservativas
Las fuerzas conservativas son aquellas que no disipan energía y, por lo tanto, conservan la energía mecánica del sistema. Ejemplos de fuerzas conservativas incluyen la fuerza gravitatoria, la fuerza elástica y la fuerza electrostática. La energía potencial asociada con estas fuerzas se puede calcular utilizando fórmulas específicas, y se puede usar para determinar la energía total del sistema.
Un ejemplo cotidiano de un sistema conservativo es un péndulo simple. Un péndulo simple consiste en una masa suspendida de una cuerda que oscila hacia adelante y hacia atrás bajo la influencia de la gravedad. En un péndulo simple, la energía potencial se convierte en energía cinética a medida que la masa se mueve hacia abajo, y luego de vuelta a energía potencial a medida que la masa se mueve hacia arriba. Debido a que la fuerza gravitatoria es conservativa, la energía mecánica total del sistema se mantiene constante y la oscilación del péndulo continúa sin cesar.
Fuerzas no conservativas
Por otro lado, las fuerzas no conservativas son aquellas que disipan energía y, por lo tanto, no conservan la energía mecánica del sistema. Estas fuerzas pueden incluir la fricción, la resistencia del aire y la resistencia del agua. Estas fuerzas disipan la energía mecánica del sistema en forma de calor u otra forma de energía no mecánica.
Un ejemplo de fuerza no conservativa es la fricción. La fricción es una fuerza que se opone al movimiento entre dos objetos en contacto. Por ejemplo, cuando se empuja un mueble por el suelo, la fricción entre el mueble y el suelo convierte parte de la energía mecánica en energía térmica, que se disipa en forma de calor. La energía mecánica del sistema se reduce a medida que el mueble se detiene debido a la fricción.
Energía Cinética:
La energía cinética es la energía asociada al movimiento de un objeto. Cuanto mayor es la masa del objeto o mayor es su velocidad, mayor es la energía cinética que posee. Matemáticamente, se expresa como:
donde:
• m es la masa del objeto.
• v es la velocidad del objeto.
Esta fórmula muestra que la energía cinética depende directamente de la masa y del cuadrado de la velocidad, lo que implica que un pequeño incremento en la velocidad puede resultar en un aumento significativo de la energía cinética.
Energía Potencial Gravitacional:
La energía potencial gravitacional es la energía almacenada en un objeto debido a su posición en un campo gravitatorio. Se refiere a la capacidad de un objeto para realizar trabajo debido a su elevación respecto a un punto de referencia (por lo general, la superficie de la Tierra u otro nivel de referencia). Se calcula con la fórmula:
donde:
• m es la masa del objeto.
• g es la aceleración debida a la gravedad (aproximadamente 9.81m/s2 en la superficie de la Tierra)
• h es la altura a la que se encuentra el objeto respecto al punto de referencia.
Esta relación indica que, al aumentar la altura h o la masa m, también aumenta la energía potencial gravitacional almacenada en el objeto.
energía potencial elástica
La energía potencial elástica de un sistema puede concebirse como la energía almacenada por un resorte comprimido o estirado. La expresión utilizada para calcular la energía elástica es:
Epelástica = 1/2kx2
Actividad N°13
Ingrese a intro en el siguiente laboratorio virtual:
Simulación de PhET Interactive Simulations, Universidad de Colorado Boulder, con licencia CC-BY-4.0 ( https://phet.colorado.edu ).
ubique el patinador en la parte superior de la pista, suetelo y haga click en el
botón verde que tiene el signo "+" y resuelva los siguientes puntos:
1. ¿Qué sucede con la energía cinética y potencial cuando al patinador está en la parte más alta de la pista?
2. ¿Qué sucede con la energía cinética y potencial cuando al patinador está en la parte más baja de la pista?
3. Dirijáse al panel superior derecho, aumente la fricción y describa lo que observa.
4. ¿Cuánto suman la energía cinética, la energía potencial gravitacional y la energía térmica?
¿Se conserva la energía mecánica? ¿Se conserva la energía?
Trabajo realizado por una fuerza
El trabajo en física se refiere al esfuerzo que se realiza para desplazar un objeto de un punto a otro, y es una de las medidas fundamentales de la energía en la física clásica. El trabajo puede ser positivo o negativo, dependiendo de la dirección en la que se desplace el objeto y de la fuerza que se aplica sobre él.
Uno de los ejemplos más comunes de trabajo en física es el trabajo que realizan los motores en los automóviles. Cuando un automóvil se desplaza en la misma dirección de la fuerza aplicada, la fuerza que imprime el motor efectua un trabajo positivo, y cuando el desplazamiento va en sentido contrario a la fuerza aplicada, tal y como sucede al frenar el automóvil, el trabajo ejercido por la fuerza de fricción es negativo.
Otro ejemplo de trabajo en la vida cotidiana es el trabajo que realizan las personas al levantar objetos. Cuando se levanta un objeto desde el suelo hasta una altura determinada, se realiza trabajo para superar la fuerza de la gravedad. Cuanto más pesado sea el objeto, más trabajo se requerirá para levantarlo.
En la industria, también hay muchos ejemplos de trabajo en física. Por ejemplo, las grúas utilizadas en la construcción realizan trabajo para levantar y mover objetos pesados. Las máquinas de corte y las herramientas eléctricas también realizan trabajo para cortar y dar forma a materiales como el metal y la madera.
En la física, el trabajo se mide en unidades llamadas joules (J). Un joule es la cantidad de trabajo necesario para mover un objeto de un kilogramo a través de una distancia de un metro, bajo la acción de una fuerza de un Newton (N). Esto significa que cuanto más grande sea la fuerza que se aplica sobre un objeto o cuanto mayor sea la distancia que se recorre, mayor será el trabajo que se realiza.
En resumen, el trabajo en física es una medida fundamental de la energía que se utiliza en una amplia variedad de situaciones de la vida cotidiana, desde levantar objetos hasta mover automóviles y utilizar máquinas en la industria. Es importante entender el concepto de trabajo para comprender cómo funcionan muchas de las cosas que nos rodean y cómo se pueden medir las fuerzas y la energía involucradas en diferentes procesos físicos.
Para describir el trabajo en física de manera matemática, se utiliza la fórmula:
donde W es el trabajo realizado, F es la fuerza aplicada, Δx es el desplazamiento y θ es el ángulo entre la dirección de la fuerza y la dirección del movimiento.
Esta fórmula indica que el trabajo es directamente proporcional a la fuerza aplicada y al desplazamiento. Sin embargo, también depende del ángulo entre la dirección de la fuerza y la dirección del movimiento. Si la fuerza se aplica en la misma dirección que el movimiento, el ángulo θ será cero y el trabajo será máximo. Si la fuerza se aplica en una dirección perpendicular al movimiento, el ángulo θ será de 90 grados y el trabajo será cero.
Relación entre trabajo y la energía cinética
Recordemo que la energía cinética es una forma de energía asociada con el movimiento de un objeto. Esta energía se define como la energía que un objeto posee debido a su velocidad y masa. El trabajo, por otro lado, se define como la cantidad de energía necesaria para mover un objeto a través de una distancia. En este artículo, exploraremos la relación entre la energía cinética y el trabajo y proporcionaremos algunos ejemplos de la cotidianidad.
La energía cinética se puede calcular utilizando la siguiente fórmula:
Ec donde es la energía cinética, "m" es la masa del objeto y "v" es su velocidad. Esta fórmula indica que la energía cinética es proporcional al cuadrado de la velocidad y a la masa del objeto.
La relación entre la energía cinética y el trabajo se puede entender a través de la siguiente observación: cuando se aplica una fuerza sobre un objeto y este se mueve una cierta distancia, la energía cinética del objeto aumenta. El trabajo realizado sobre el objeto es igual a la energía cinética ganada por el objeto. En otras palabras, el trabajo es la cantidad de energía que se ha transferido al objeto para que este adquiera una determinada velocidad. En este orden de ideas la expresión que relaciona el trabajo y la energía cinética es:
Wneto = 1/2 mvf2 - 1/2 mvi2
Wneto = Ecf - Eci = ΔEc
Algunos ejemplos cotidianos de la relación entre la energía cinética y el trabajo son los siguientes:
• Al empujar una caja por una distancia, se realiza un trabajo sobre ella que aumenta su energía cinética, lo que le permite moverse más rápido.
• Al lanzar una pelota, se realiza un trabajo sobre ella que aumenta su energía cinética, lo que le permite viajar más lejos y más rápido.
• Al frenar un automóvil, se realiza un trabajo que disminuye su energía cinética, lo que le permite detenerse. Considerando que en este caso el sistema perdió energía, el trabajo efectuado por la fuerza es negativo.
Relación entre trabajo y la energía potencial gravitacional
La relación entre la energía potencial y el trabajo se puede entender a través de la siguiente observación: cuando un objeto se mueve en un campo de fuerza, como la gravedad, la energía potencial del objeto cambia. Si se realiza un trabajo sobre el objeto, la energía potencial del objeto puede convertirse en energía cinética o en otra forma de energía. En otras palabras, el trabajo puede transferir energía potencial a otras formas de energía. Tengase en cuenta que la siguiente expresión que se utilizará para calcular la energía potencial gravitacional, solo es aplicable para objetos que estén cerca de la superficie terrestre:
Epg = mgh
Así pues la expresión que relaciona el trabajo neto con la energía potencial gravitacional es:
Wneto = mghf - mghi
Wneto = Epgf - Epgi = ΔEpg
Algunos ejemplos cotidianos de la relación entre la energía potencial y el trabajo son los siguientes:
• Al levantar un objeto del suelo, se realiza un trabajo sobre él que aumenta su energía potencial debido a su altura con respecto al suelo.
• Al soltar un objeto desde una altura, la fuerza peso realiza trabajo sobre él convirtiendo su energía potencial en energía cinética, lo que le permite moverse más rápido.
• Al lanzar un objeto hacia arriba, se realiza un trabajo sobre él que aumenta su energía potencial a medida que sube, antes de que su energía potencial se convierta en energía cinética cuando comienza a caer.
Potencia
La potencia en física se define como la cantidad de trabajo realizado o la energía transferida por unidad de tiempo. Es una magnitud que indica qué tan rápido se efectúa un trabajo o se transfiere energía. En el Sistema Internacional de Unidades (SI), la potencia se mide en vatios (W), donde:
1 W = 1 Joule/s
Las fórmulas más comunes para calcular la potencia son:
P = W/t
donde:
• P es la potencia.
• W es el trabajo realizado en Joules
• t es el tiempo en segundos (s).
Potencia en términos de fuerza y velocidad (en movimientos rectilíneos uniformes):
P = F.v
donde:
• F es la fuerza.
• v es la velocidad (en metros por segundo, m/s).
Actividad N°14
1. Ingresa al siguiente recurso para practicar lo aprendido sobre trabajo y el teorema de la conservación de la energía mecánica.
Actividad N°15
Considere para todos los ejercicios que la intensidad de la gravedad es de 10m/s2.
Responda las preguntas 1-3 de acuerdo a la siguiente información
Condiciones: No hay fuerzas disipativas
Una esfera se suelta desde el reposo sobre una superficie curva como se ilustra en la figura.

1. ¿Cuál es la energía cinética del sistema en h1?
2. Si h = 10m, h3 = 20m y la masa de la bolita roja es 2kg. Determina la velocidad
inicial de la bolita para que llegue a h3.
3. Considerando los datos del punto anterior y que h1=5m y h2=7m, encuentre:
a. La energía potencial y cinética en h1.
b. La energía potencial y cinética en h2.
4. Daniel desea conocer la longitud mínima que debe
comprimir el resorte para que la bola de masa "m" llegue
justamente hasta la altura "h".
Condiciones: No hay fuerzas disipativas

Encuentre una expresión en términos de "m", "g", "h" y "k" que determine la distancia que debe elongarse el resorte.
5. Andrés desea apilar 5 bloques iguales de la siguiente manera.
Condiciones: No hay fuerzas disipativas

Calcule el trabajo requerido para ello.
6. Un bloque de 2kg se desplaza sobre una superficie horizontal que tiene una fuerza de fricción de 10N. Si la fuerza aplicada es de 120N, ¿Cuál es la aceleración del bloque? ¿Cuál es la velocidad del bloque al cabo de 5s, 10s y 25s?¿Cuál es la distancia recorrida por el bloque al cabo de 5s, 10s y 25s?
7.Mangüirry aplica una fuerza de 150N sobre un bloque de madera que tiene una masa de 10kg. Sí la superificie tiene un coeficiente de rozamiento de 0.3 y el bloque se mueve horizontalmente, ¿Cuál es la fuerza resultante? ¿Cuál es la aceleración del bloque? ¿Cuál es la velocidad del bloque al cabo de 5s, 10s y 25s?¿Cuál es la distancia recorrida por el bloque al cabo de 5s, 10s y 25s? Represente el movimiento utilizando las gráficas de (X vs t),(V vs t) y (a vs t)?
8. Toño es una tortuga que transporta una caja de cartón del punto A al punto D, tal y como se aprecia a continuación:
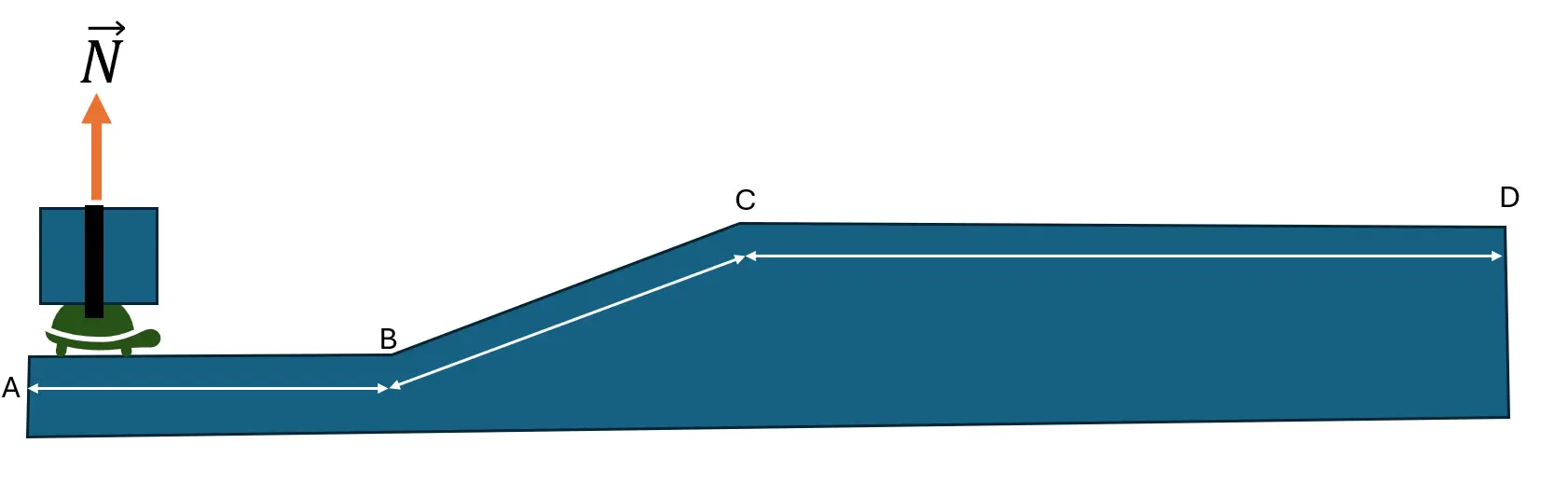
Responda las siguientes preguntas teniendo en cuenta la información anterior:
a. ¿Cuales son las fuerzas que actúan sobre la caja? Realice un diagrama de cuerpo libre.
b. ¿Cuánto trabajo efectúa la normal de A hasta B? Justifique su respuesta.
c. ¿Cuánto trabajo efectúa el peso de A hasta B? Justifique su respuesta.
d. ¿Cómo es el trabajo que fectúa la fuerza que desplaza la caja del punto A al B.? ¿Nulo?¿Negativo?¿Positivo? justifique su respuesta.
e. ¿Cómo es el trabajo que fectúa la fuerza que desplaza la caja del punto B al C.? ¿Nulo?¿Negativo?¿Positivo? justifique su respuesta.
f. ¿Cómo es el trabajo que fectúa la Normal cuando la tortuiga se desplaza del punto B al C.? ¿Nulo?¿Negativo?¿Positivo? justifique su respuesta.
g. ¿Cómo es el trabajo que fectúa el peso cuando toño se desplaza del punto B al C.? ¿Nulo?¿Negativo?¿Positivo? justifique su respuesta.
h. ¿Cuál es la única fuerza que efectúa trabajo cuando la tortuga se desplaza del punto C al D.? justifique su respuesta.
9. Mangüirry trata de mover horizontalmente una roca de 400kg y para ello aplica una fuerza de 2000N. Si la superficie tiene un coeficiente de rozamiento de 0.5, ¿Cuál es la fuerza resultante? ¿Mangüirry logra mover la roca? ¿Cuál es la aceleración de la roca?¿Cuánto trabajo efectúa la fuerza que aplica Mangüirry?¿Cuánto trabajo ejerce la fuerza de fricción? ¿Cuánto trabajo efectúa la fuerza resultante? Represente el movimiento utilizando las gráficas de (X vs t),(V vs t) y (a vs t)?
10.Mangüirry se dirige a abordar el avión y arrastra su maleta como se aprecia en la siguiente imagen:
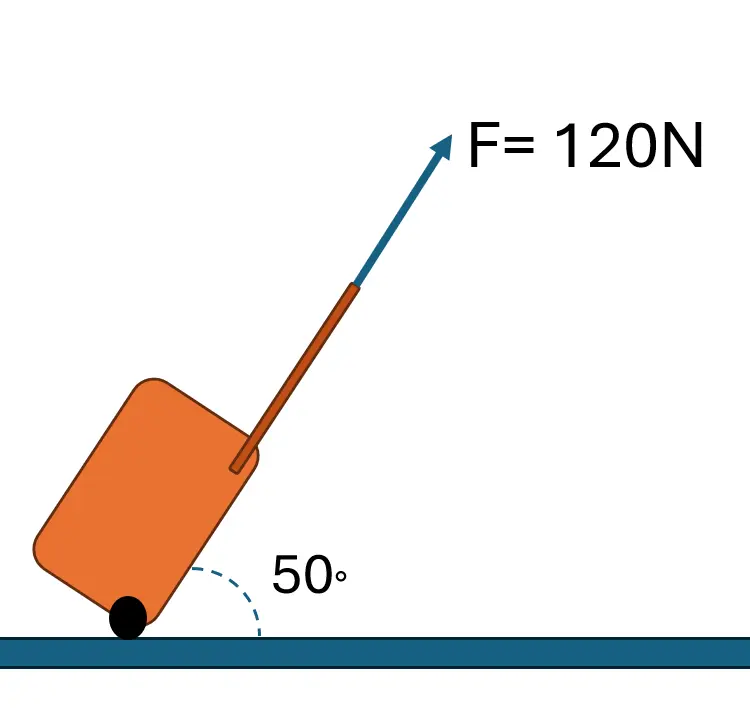
Si la maleta tiene una masa de 20kg y la fuerza de fricción es de 50N, ¿Cuál es la fuerza resultante? ¿Cuánto trabajo efectúa la fricción? ¿Cuánto trabajo efectúa la fuerza "F"? ¿Cuál es la aceleración de la maleta? ¿Cuál es la velocidad de la maleta al cabo de 5s, 10s y 25s?¿Cuál es la distancia recorrida por la maleta al cabo de 5s, 10s y 25s? Represente el movimiento utilizando las gráficas de (X vs t),(V vs t) y (a vs t)?
11. Dado el siguiente montaje:
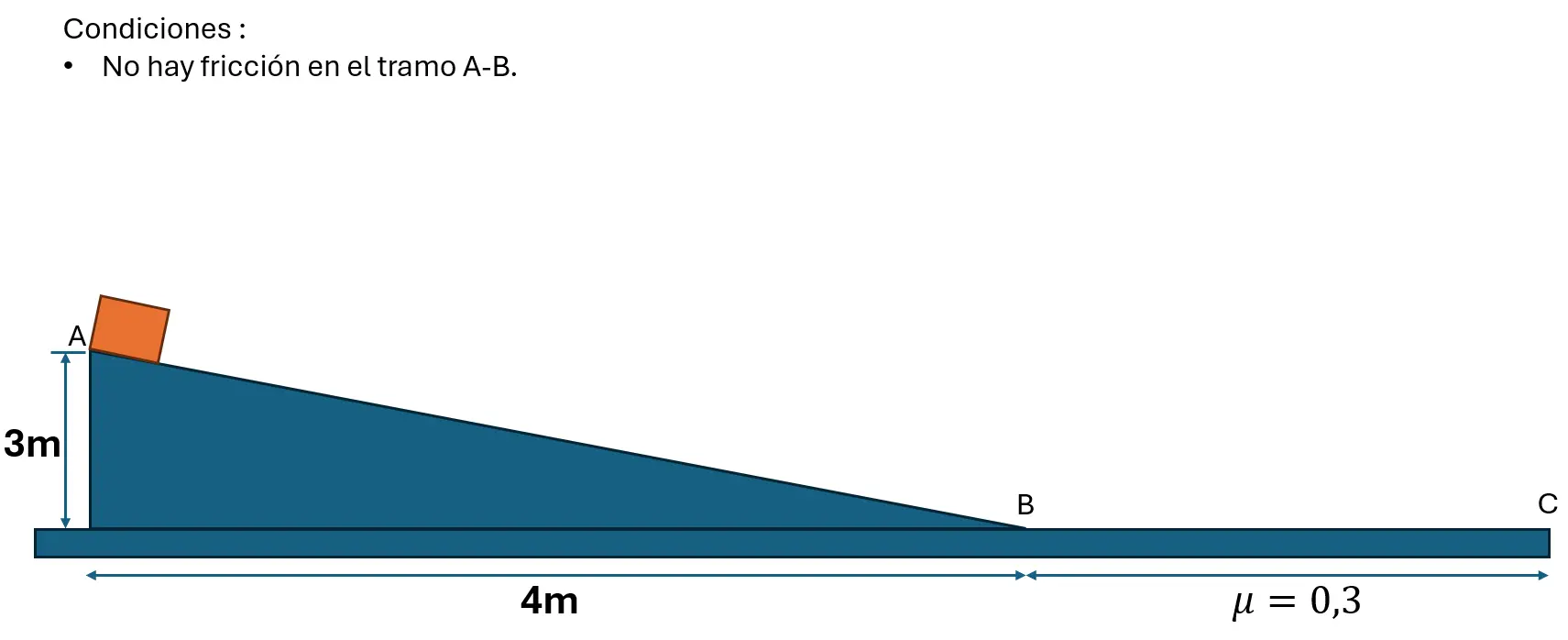
a. Dibuje el diagrama de cuerpo libre de las fuerzas que actún en el bloque.
b. ¿Cuál es la aceleración que experimenta el bloque?
c. ¿Cuál es la velocidad que alcanza el bloque en el punto B?
d. ¿Cuál es la aceleración que experimenta el bloque en el tramo B-C?
e. ¿Cuál es la velocidada del bloque al cabo de 2s, 3s, 4s, 5s, 10s, 20s y 30s?
f. Cuando el bloque está en el tramo B-C, ¿cuánto tarda en detenerse?
g. Realice un bosquejo (X vs t), (v vs t) y (a vs t) del movimiento del bloque.
12. Un trabajador eleva una carga de 50kg a una altura de 3m en 4s. Calcula la potencia promedio desarrollada, considerando que la aceleración de la gravedad es g= 9.8m/s 2
13. Mangüirry aplica Una fuerza "F" en la misma dirección del movimiento de un móvil que se desplaza en línea recta y registra los siguientes datos:
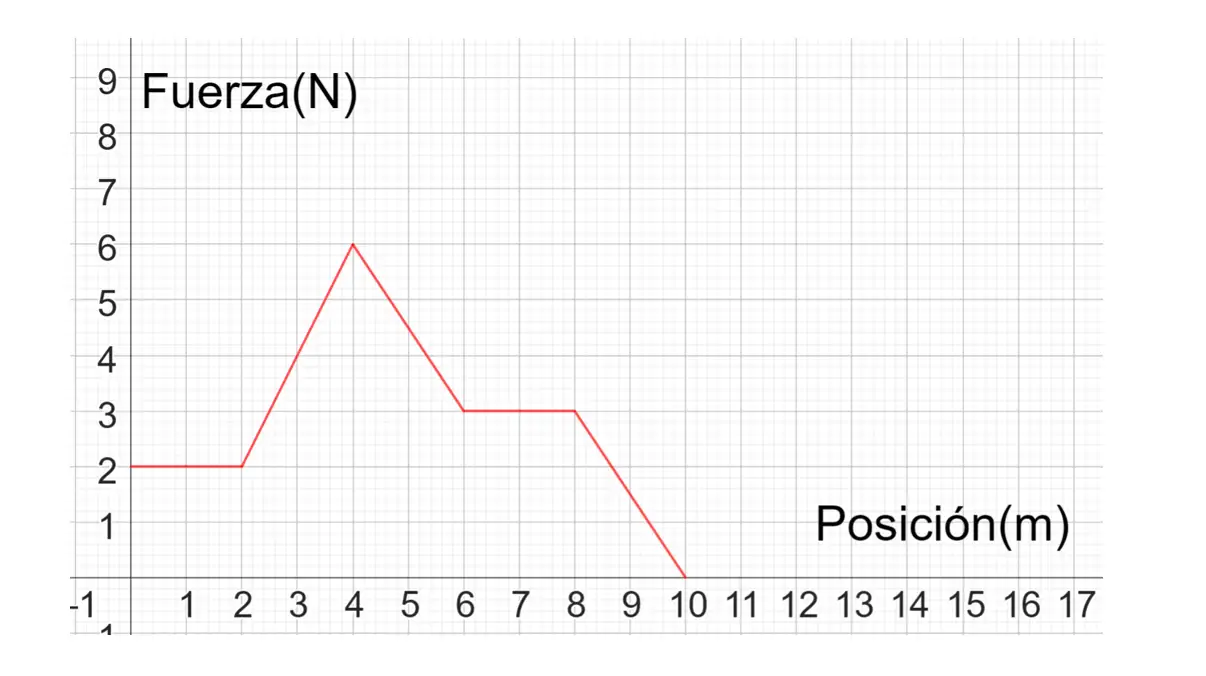
a. ¿Cuál es el trabajo efectuado por la fuerza F cuando el móvil:
i. Se desplaza de 0 a 2m.
ii. Se desplaza de 2 a 4m.
iii. Se desplaza de 4 a 6m.
iv. Se desplaza de 6 a 8m.
v. Se desplaza de 8 a 10m.
vi. Se desplaza de 0 a 10m.
b. Teniendo en cuenta que el móvil al pasar por la posición cero tiene una energía cinética de 100J, ¿Cuál es la energía cinética del móvil al pasar por la posición 10m?
c. ¿Calcule la velocidad del móvil al pasar por la posición 10m?
14. Un estudiante sube unas escaleras cargando una mochila pesada. Si lo hace en menor tiempo que su compañero, ¿qué se puede afirmar sobre su potencia?
A. Su potencia es menor, porque aplicó menos fuerza.
B. Su potencia es mayor, porque realizó el mismo trabajo en menos tiempo.
C. Su potencia es la misma, porque el trabajo no depende del tiempo.
D. Su potencia es menor, porque el trabajo depende solo de la altura.
15. Dos motores realizan el mismo trabajo, pero el motor A lo hace en la mitad del tiempo que el motor B. ¿Cuál de las siguientes afirmaciones es correcta?
A. El motor A tiene la mitad de la potencia del motor B.
B. El motor A tiene el doble de la potencia del motor B.
C. Ambos motores tienen la misma potencia.
D. El motor A realiza el doble de trabajo que el motor B.
16. Un ciclista aplica una potencia constante al pedalear en una carretera plana. Si la resistencia del aire aumenta, ¿qué sucede con su velocidad si mantiene la misma potencia?
A. Aumenta, porque la potencia aplicada no depende de la resistencia.
B. Se mantiene constante, porque la potencia aplicada sigue siendo la misma.
C. Disminuye, porque parte de la potencia se usa para vencer la resistencia del aire.
D. No cambia, ya que la potencia solo depende de la masa del ciclista.
17. Una bombilla de 100 W y otra de 60 W están encendidas durante una hora. ¿Cuál de las siguientes afirmaciones es correcta respecto al consumo de energía?
A. La bombilla de 100 W consume más energía porque su potencia es mayor.
B. Ambas bombillas consumen la misma energía porque están encendidas el mismo tiempo.
C. La bombilla de 60 W consume más energía porque dura más encendida.
D. La bombilla de 100 W consume menos energía porque es más eficiente.
Colisiones
La colisión de objetos es un fenómeno común en la física, y se clasifican en diferentes tipos según la cantidad de energía cinética que se conserva después de la colisión. Los tres tipos principales de colisiones son elásticas, inelásticas y perfectamente inelásticas. A continuación, describiremos cada uno de estos tipos de colisiones.
Colisiones elásticas
Una colisión elástica es una colisión en la que se conserva la energía cinética total del sistema. Esto significa que después de la colisión, la suma de las energías cinéticas de los objetos involucrados es la misma que antes de la colisión. En una colisión elástica, los objetos se separan después de la colisión y no hay deformación permanente en ninguno de los objetos. En otras palabras, la energía mecánica total del sistema se conserva.
Un ejemplo de una colisión elástica es cuando dos bolas de billar se golpean entre sí. Antes de la colisión, cada bola tiene una cierta cantidad de energía cinética. Después de la colisión, cada bola se mueve en una dirección diferente, pero la suma de sus energías cinéticas sigue siendo la misma que antes de la colisión.
Por otro lado, es importante mencionar que en una colisión de este tipo también se conserva la cantidad de movimiento del sistema, en otras palabras, la suma de las cantidades de movimiento de los cuerpos antes de colsionar es igual a la suma de las cantidades de movimiento después de la colisión.
Colisiones inelásticas
Una colisión inelástica es una colisión en la que parte de la energía cinética del sistema se pierde en forma de calor o deformación. En una colisión inelástica, los objetos se juntan después de la colisión y se produce una deformación permanente en uno o ambos objetos. En una colisión inelástica, la energía cinética total del sistema no se conserva.
Un ejemplo de una colisión inelástica es cuando un coche choca contra una pared. Antes de la colisión, el coche tiene una cierta cantidad de energía cinética. Después de la colisión, el coche se deforma y parte de la energía cinética se pierde en forma de calor y deformación.
Un aspecto tan importante como el entarior, es tener en cuenta que en este caso si se conserva la cantidad de movimiento del sistema, tal y como sucede en una colisión elástica.
Colisiones perfectamente inelásticas
Por último, una colisión perfectamente inelástica es una colisión en la que los objetos involucrados se juntan y se mueven juntos después de la colisión. En una colisión perfectamente inelástica, la energía cinética total del sistema no se conserva; pero si la cantidad de movimiento del sistema.
Un ejemplo de una colisión perfectamente inelástica es cuando dos bloques de arcilla se pegan entre sí después de chocar. Antes de la colisión, cada bloque tiene una cierta cantidad de energía cinética. Después de la colisión, los bloques se pegan y se mueven juntos, y la energía cinética total del sistema no se conserva.
Laboratorio virtual
Actividad # 16
Ingrese al laboratorio virtual en el apartado intro, seleccione la casilla más datos y resuelva en el cuaderno los siguientes interrogantes:
Simulación de PhET Interactive Simulations, Universidad de Colorado Boulder, con licencia CC-BY-4.0 ( https://phet.colorado.edu ).
1. Describa el movimiento de dos masas iguales después de colisionar a la misma velocidad.
2. Describa el movimiento de dos masas iguales después de colisionar a diferentes velocidades.
3. Describa el movimiento de dos masas diferentes después de colisionar a la misma velocidad.
4. Describa el movimiento de dos masas diferentes después de colisionar a diferentes velocidades.
5. Asigne valores arbitrarios para la masa, la velocidad y determine, ¿qué sucede con la energía cinética del sistema antes y después de la colisión?
6. Asigne valores arbitrarios para la masa, la velocidad y determine, ¿qué sucede con el momentum o cantidad de movimiento del sistema antes y después de la colisión?
7. Considere la información obtenida al resolver los puntos anteriores y construya una lista de
conclusiones.
Actividad # 17
Ingrese al siguiente recurso y aplique lo aprendido sobre colisiones
